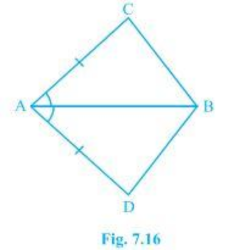
1. In quadrilateral ACBD, AC = AD and AB bisect ∠A (see Fig. 7.16). Show that ΔABC≅ ΔABD. What can you say about BC and BD?
Ans:
It is given that AC and AD are equal i.e. AC = AD and the line segment AB bisects ∠A.
We will have to now prove that the two triangles ABC and ABD are similar i.e. ΔABC ≅ ΔABD
Proof:
Consider the triangles ΔABC and ΔABD,
(i) AC = AD (It is given in the question)
(ii) AB = AB (Common)
(iii) ∠CAB = ∠DAB (Since AB is the bisector of angle A)
So, by SAS congruency criterion, ΔABC ≅ ΔABD.
For the 2nd part of the question, BC and BD are of equal lengths by the rule of C.P.C.T.
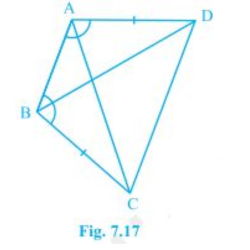
2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig. 7.17). Prove that
(i) ΔABD ≅ ΔBAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.
Ans:
The given parameters from the questions are ∠DAB = ∠CBA and AD = BC.
(i) ΔABD and ΔBAC are similar by SAS congruency as
AB = BA (It is the common arm)
∠DAB = ∠CBA and AD = BC (These are given in the question)
So, triangles ABD and BAC are similar i.e. ΔABD ≅ ΔBAC. (Hence proved).
(ii) It is now known that ΔABD ≅ ΔBAC so,
BD = AC (by the rule of CPCT).
(iii) Since ΔABD ≅ ΔBAC so,
Angles ∠ABD = ∠BAC (by the rule of CPCT).
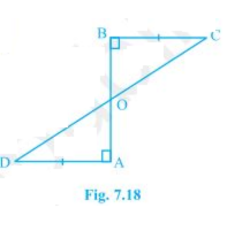
3. AD and BC are equal perpendiculars to a line segment AB (see Fig. 7.18). Show that CD bisects AB.
Ans:
It is given that AD and BC are two equal perpendiculars to AB.
We will have to prove that CD is the bisector of AB
Now,
Triangles ΔAOD and ΔBOC are similar by AAS congruency since:
(i) ∠A = ∠B (They are perpendiculars)
(ii) AD = BC (As given in the question)
(iii) ∠AOD = ∠BOC (They are vertically opposite angles)
∴ ΔAOD ≅ ΔBOC.
So, AO = OB (by the rule of CPCT).
Thus, CD bisects AB (Hence proved).
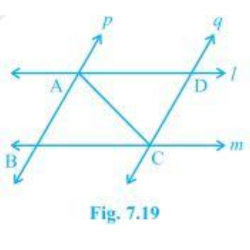
4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig. 7.19). Show that ΔABC ≅ ΔCDA.
Ans:
It is given that p || q and l || m
To prove:
Triangles ABC and CDA are similar i.e. ΔABC ≅ ΔCDA
Proof:
Consider the ΔABC and ΔCDA,
(i) ∠BCA = ∠DAC and ∠BAC = ∠DCA Since they are alternate interior angles
(ii) AC = CA as it is the common arm
So, by ASA congruency criterion, ΔABC ≅ ΔCDA.
